PREVIOUS PAGE < > NEXT PAGE





|
WIND TURBINES
|
SOLAR
|
|
+ No fuel cost
|
+ No fuel cost
|
|
+ Zero emissions during operation
|
+ Zero emissions during operation
|
|
+ Reasonable cost ($/kWh)
|
+ Reasonable cost ($/kWh) for Thermal
|
|
+ They look pretty…
|
+ Supply (sun) in phase with demand
|
|
+ Sites can be multi-use (farm+wind turbine)
|
+ Easier to predict
|
|
More cost efficient to build large wind farms
|
Generally better when installations are distributed
|
|
- Resource is variable (and hard to predict)
|
- Centralized installations take up a lot of space
|
|
- Best sites are not generally near population centers
|
- High cost ($/kWh) for Electricity
|
A summary comparison of the pros and cons of wind and solar as energy sources
AVAILABILITY OF SOLAR ENERGY
Similar to wind, it is important to understand how much solar energy is available at a particular geographical location as well as how much of that energy varies with time. This requires knowing the intensity of energy arriving from the sun and then determining how much of that intensity is able to reach the earth's surface. This intensity change is known as insolation. Average insolation is lower than the amount available outside the atmosphere due to absorption and diffraction of sunlight in the atmosphere and is affected by many factors, including air pollution, weather, time of day, time of year (the distance between the earth and sun), and latitude.
In general, insolation values are lower during the winter than those in the summer. This is especially true in the case of high latitude countries (between 46° and 54° north latitude) because of the shorter days and the more oblique angle at which the sunlight hits horizontal surfaces.
Energy from the Sun that Reaches the Outside of Earth's Atmosphere
The sun can be treated as a black body so that the energy flux that it emits is a function of its temperature and proportional to the Stephan-Boltzmann constant. Since the sun has an approximate temperature of 5770K, the resulting energy flux (per unit area) is:
-
|
Esun = σT4 = 6.28x107 W/m2
|
where σ is the Stephan-Boltzmann constant,
σ=5.67x10-8 W/m2K
Tsun = ~5770K = surface temperature of the sun
|
However, not all of this energy reaches the Earth's surface. Some of this energy radiates in an entirely different direction from earth and the intensity of the energy flux that is headed our direction degrades as a function of the square of the distance so that by the time it reaches the outside of Earth's atmosphere, the average intensity of the light is:
-
|
Esunearth = Esun(Dsun/d)2 =1367 W/m2
|
where Dsun = 7x108 m = the diameter of the sun
d ~=1.5x1011 m = the distance from the sun to earth
|
The value 1367 W/m2 is known as the solar constant, Io – even though it isn’t really a constant value. This number varies with changes in the sun’s surface, such as solar flares and sun spots, but it is primarily affected by the distance between the sun and the earth which continually changes as the earth moves through its orbit. The daily solar constant is determined by:
-
|
Idaily = 1367[1+0.034cos(2πN/365)]
|
where N is the day number from the Julian Calendar
|
The energy that reaches the Earth, however, is not all equal; the energy flux can be further broken down by wavelength. The Sun, being very hot, emits waves that are short but high frequency, while the Earth emits longer, lower frequency waves. As discussed earlier, the distribution of wavelengths emitted by the Sun plays a role in the Greenhouse Effect (see Climate Change) but it also plays a role in the efficiency of solar collectors which will be discussed later (see Solar Photovoltaics). For the Earth and the Sun, a summary of the energy break down is shown in the figure below.
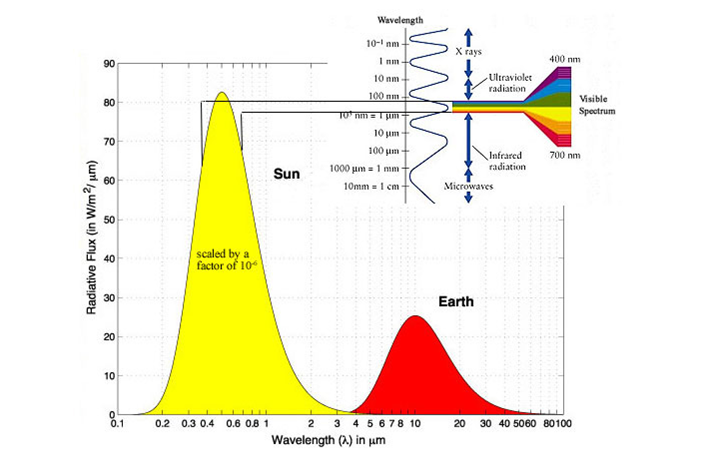
Figure 1: Wavelength Distribution
Energy from the Sun that Reaches the Surface of the Earth
As it passes through the atmosphere, the energy from the sun is absorbed and diffracted so the amount that actually reaches the Earth’s surface is significantly reduced. Of the light that reaches earth, some of it is by direct transmission and some is by diffuse transmission, and their sum makes up global insolation. The transmission of solar energy through the atmosphere is primarily effected by:
- time of day
- time of year
- atmosphere
- aerosols
- dust
- clouds
|

|
Figure 2: Solar Radiation at the Earth's Surface
The first two factors are based on the relative positions of the earth and sun (in terms of angles and distance), which are both well understood. They are discussed in Section II below ("Position of the Sun by..."). Other factors include the Air Mass number. The Air Mass number accounts for the loss of solar energy due to the atmosphere, while the other variables are emperical, based on pollution and weather in a given location in which their effects can be estimated using the equation below. This equation yields the total transmission of solar energy through the atmosphere (aka the insolation intensity).
|
I = Ioe ^[–AM(τaeresol + τwater + τozone + τCO2+ τRayleigh)]
|
where AM = the Air Mass Number
AM = CB/AB (see figure below, [1])
= 1/cosθz (correct for small θz)
|
The previous Air Mass equation becomes incorrect for large values of the zenith angle (shown below, figure 2) because it predicts an infinitely large air mass number when the sun is at the horizon and the zenith angle is 90. To account for the earth's curvature, the following somewhat more complex equation can be used when the sun is near the horizon.
AM = (1/(cos (zenith angle)+0.50572*(96.07995-zenith angle)^-1.36364))

Figure 3: Zenith Angle
Another factor that affects the global insolation is the atmosphere transmittance, which can be approximated for a clear sky (pollution free) within a 5% accuracy by using the following equation:
t,atm = 0.5( e^(-0.65*AM)+e^(-0.095*AM))
The variations in solar energy discussed above can clearly be seen in the following figure [4]. It shows the solar power available on a horizontal surface in Ithaca, New York over the course of 14 years. The upper line is the power available outside the earth's atmosphere/day, while the points below represent the power that actually reached the surface each day.
- The shape of the data is due to the relative positions of the earth and sun (see Section II)
- The gap between the real data and the calculated available energy is due to atmospheric losses
- The scatter in the data illustrates the effects of aerosols, clouds and dust and how the insolation varies with different concentrations

Figure 4: Daily Solar Power
POSITION OF THE SUN BY TIME OF DAY AND SOLAR ANGLES

Figure 5: Annual Sun Orientation
The position of the sun is dictated by both the time of day and the time of year. Simply put, solar angle calculations are done in solar time. Solar time is adjusted from standard time so that the sun is due south at solar noon. Solar time is synchronous with local standard time but leads or lags standard time because of two factors. One factor is the difference between the local longitude and the standard longitude value that defines the local time zone. The other factor is the equation of time (ET), which exists due to the earth's path around the sun being an ellipse rather than a circle. Standard longitudes are measured in increments of 15º with 0º being located in Greenwich, England.
To further understand solar geometry, we must consider the following geometric terms: zenith angle, solar altitude, surface azimuth angle, solar azimuth, surface slope, declination and hour angle. Solar altitude is the angle of the sun above the horizon. The zenith angle is the angle between a line from the sun and a line orthogonal to the horizontal surface. The solar azimuth is the angle between the direction of the sun and due south. The surface azimuth is the angle between the direction of the surface and due south. Declination is the angle between the line of the sun and the plane of the equator. The hour angle is the degrees of the earth’s rotation before and after solar noon.
When considering the surface of a solar device, the relationship between this surface and the position of the sun can give us the proportion of incoming energy that is available to the device. Therefore, the orientation of the device becomes a major factor. The orientation of the device depends on essentially two factors: angle of incidence, and tilt angle. The angle of incidence is the angle between a beam of sunlight and the direction normal to the surface, while the tilt angle is the angle between the device and the horizontal; however, the angle of incidence is a function of the tilt angle.
Each of the angles defined above may be seen below in figure 6 and their respective symbols may be found below in table 1.

Figure 6: Various Solar Angles
The efficiency of a solar collecting device greatly depends on its orientation relative to the Sun. As the angle of incidence is reduced, the amount of sunlight hitting the collector increases simply because the projected area orthogonal to the incoming sunlight increases. A simple diagram of this correlation may be found below in figure 7. One can see from this diagram how much of an impact minimizing the angle of incidence has on possible power production.
 Figure 7: Incidence Angle's Effect on Efficiency
Figure 7: Incidence Angle's Effect on Efficiency
Equations
SOLAR TIME
tsol = tstd + (1/15)x(Lstd – Lloc) + ET
EQUATION OF TIME
ET = –7.3412sin(q) + 0.4944cos(q) – 9.3795sin(2q) – 3.2568cos(2q) – 0.3179sin(3q) – 0.0774cos(3q) – 0.1739sin(4q) – 0.1283cos(4q)
DECLINATION
d = 23.45sin[360(284 + N)/365]
SOLAR ALTITUDE AT SOLAR NOON
amax = 90 – f + d (at solar noon)
HOUR ANGLE (W)
W= hour * 15-180
hour: given in 24hr decimal time.
SOLAR AZIMUTH
sin(gs) = cos(d) sin(w) / cos(a)
ANGLE OF INCIDENCE
cos(qi) = sin(a) cos(b) + cos(a) sin(b) cos(g -gs)
ANGLE OF INCIDENCE FOR A FLAT SURFACE, b = 0
cos(qi) = sin(a)
ANGLE OF INCIDENCE FOR A VERTICAL SURFACE, b = 90
cos(qi) = cos(a) * cos (g-gs)
ANGLE OF INCIDENCE FOR A SOUTH-FACING SURFACE, g = 0
cos(qi) = sin(a) * cos(b) + cos(a) * sin(b) * cos(gs)
HOURLY BEAM RADIATION FOR A HORIZONTAL SURFACE, b = 0
Ih = I * cos(qz)
HOURLY BEAM RADIATION FOR A TILTED SURFACE, b ~= 0
Ib = I * cos(qi)
Table 1: Variables
tsol
|
solar time [hours]
|
a
|
solar altitude [degrees]
|
tstd
|
standard time [hours]
|
qz
|
zenith angle [degrees]
|
Lstd
|
standard longitude [degrees]
|
w
|
hour angle [degrees]
|
Lloc
|
local longitude [degrees]
|
gs
|
solar azimuth [degrees]
|
f
|
local lattitude [degrees]
|
g
|
surface azimuth [degrees]
|
ET
|
equation of time [minutes]
|
b
|
tilt angle [degrees]
|
q
|
360N/365 [degrees] or 2piN/365 [radians]
|
qi
|
angle of incidence [degrees]
|
N
|
Julian Day
|
Ih
|
radiation for horizontal surface [W/m2]
|
d
|
declination [degrees]
|
Ib
|
radiation for tilted surface [W/m2]
|

There are also some very interesting tools that can calculate solar position and angles.
Example: Solar Flux Reaching a Surface
Example 9-2 from [1]
Q. A normal beam of radiation with an intensity I=350 W/m2 .What is the flux reaching a solar surface facing due south, tilted south by 25° , on the summer solstice at 11 a.m. in Detroit (L=42° N) ?
A. Since the surface faces due south the surface azimuth angle g is 0. On the summer solstice, the hour angle is -15° at 11 a.m. and the declination d =23.45°. Using the above equations the solar altitude can be solved for as
a =asin(sindsinf +cosdcosfcosw)=asin(sin(23.45)sin(42)+cos(23.45)cos(42)cos(-15)= 67.6 °
The solar azimuth can be found as
gs =asin(cosdsinw/cosa)= asin(cos(23.45)sin(-15)/cos(67.6)=-38.6 °
Once the altitude and elevation are known, the angle of incidence can be found as
qi = acos(sinacosb + cosasinbcos(g -gs))=acos(sin(67.6)cos(25)+cos(67.6)sin(25)cos(38.6))=15.5°
Finally the energy flux into the surface is the intensity multiplied by the cosine of the angle of incidence
Is=I*cos(qi)=(350)cos(15.5)=337 W/m2
Reference:
-
Vanek, Francis M. and Albright, Louis D., Energy Systems Engineering - Evaluation and Implementation, McGraw Hill, New York, 2008.
-
Solar Band of Images - http://www.pvesco.com/Images/Drago2.JPG, http://www.jewishjournal.com/geekheeb/item/stolen_solar_panels_turn_up_online_20080924/http://www.jewishjournal.com/geekheeb/item/stolen_solar_panels_turn_up_online_20080924/, http://www.aerospaceguide.net/solar_system/our_sun.gif, http://www.manywallpapers.com/space-wallpapers/earth/earth-and-sun.html, http://www.trec-uk.org.uk/images/schott_parabolic_trough.jpg
-
Sun Image - http://www.swpc.noaa.gov/primer/primer.html
-
Blackbody Radiation Image - http://www.webexhibits.org/causesofcolor/images/content/29z.jpg
-
Daily Solar Radiation Image - http://www.colorado.edu/geography/class_homepages/geog_3251_sum08/05_solar_radiation.jpg
-
Earth's Orbit Image - http://solar.steinbergs.us/images/jpgs/earth-rotate-R-sun.jpg
-
Position of the Sun Image - http://4.bp.blogspot.com/_a6h7HUJUQfg/SNj5Alr_ccI/AAAAAAAAAR8/zFm5g1HQgAM/s1600-h/SolarDeclination.jpg
-
http://www.unbf.ca/arts/IDS/Dev/faculty.html
q
Comments (1)
Brady Kappius said
at 11:10 am on Nov 2, 2010
"Finally the energy flux into the surface is the intensity divided by the cosine of the angle of incidence"
Divided by or multiplied?
You don't have permission to comment on this page.